Inference for Regression

Dr. Elijah Meyer

NC State University
ST 511 - Fall 2025

2025-11-05

Checklist

– Quiz released this afternoon (due Sunday)

– Homework released Friday (due Friday)

– Statistics experience released

– Expect take-home grades by tonight

– Final Exam is Dec 8th at 3:30 (expect an email this afternoon)

AI

Thinking about your future

– Calculators don’t make you good at math… LLMs don’t make good researchers

– If you work with private data, you can’t use LLMs

– If you only know how to use LLMs, your skillset is not marketable… it’s sloppy (especially in statistics)

– LLMs are trained on a lot of data (some correct/some not). Think of your last Google Search.

AI

Thinking about you as a student

We (very often) don’t use AI as a learning tool, and instead use it as a producer

Once you have the foundation, this tool can really help you

This is an introduction to statistics course (we are building the foundation)

AI

Thinking about you as a student

… and I know how stressed you are with time (I was a student just a couple years ago)

– but this hurts you now

– and hinders where you are going

Warm Up

How can we summarize these data?

Summary statistics

– correlation (r)

– slope + intercept (fit a line)

Correlation

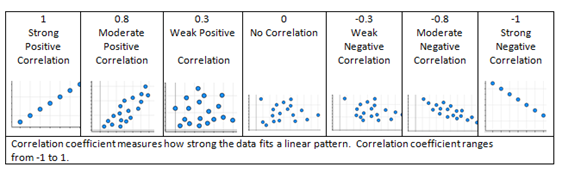
In R

Let’s find the correlation coefficient between our two variables

syntax: cor(x, y)

airquality |> 
  summarise(corr = cor(Wind, Temp, use = "complete.obs"))
        corr
1 -0.4579879

Fit a line

… and talk about the slope and the intercept

The line

Let me (re) introduce you to:

Population level: \(y = \beta_o + \beta_1*x + \epsilon\)

Sample: \(\hat{y} = \hat{\beta_o} + \hat{\beta_1}*x\)

In R

model1 <- lm(Wind ~ Temp, data = airquality)

tidy(model1)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   23.2      2.11       11.0  4.90e-21
2 Temp          -0.170    0.0269     -6.33 2.64e- 9

– Prediction

– Interpretation

Why mean response?

Statistical Inference

We can also test for a linear relationship between x and y…

What would the null and alternative hypotheses be?

Null and alternative

\(H_o: \beta_1\) = 0

\(H_a: \beta_1 \neq 0\)

Assumptions

– Independence (we know how to check this)

– Linear relationship (two ways to check this)

– Equal Variance (new way to check this)

– Normality or residuals (we know how to check this)

Independence

Linear relationship

Does it make sense?

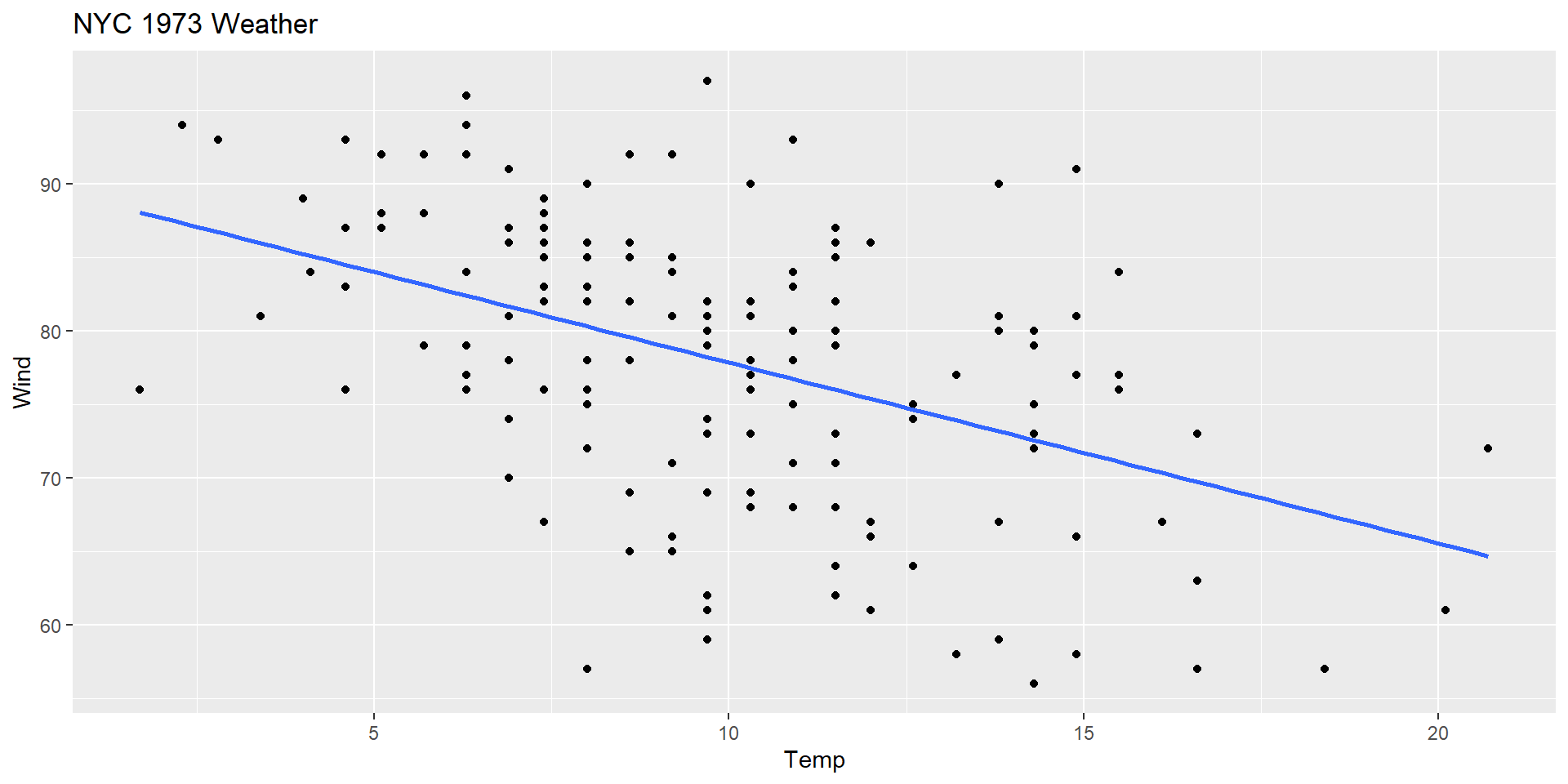
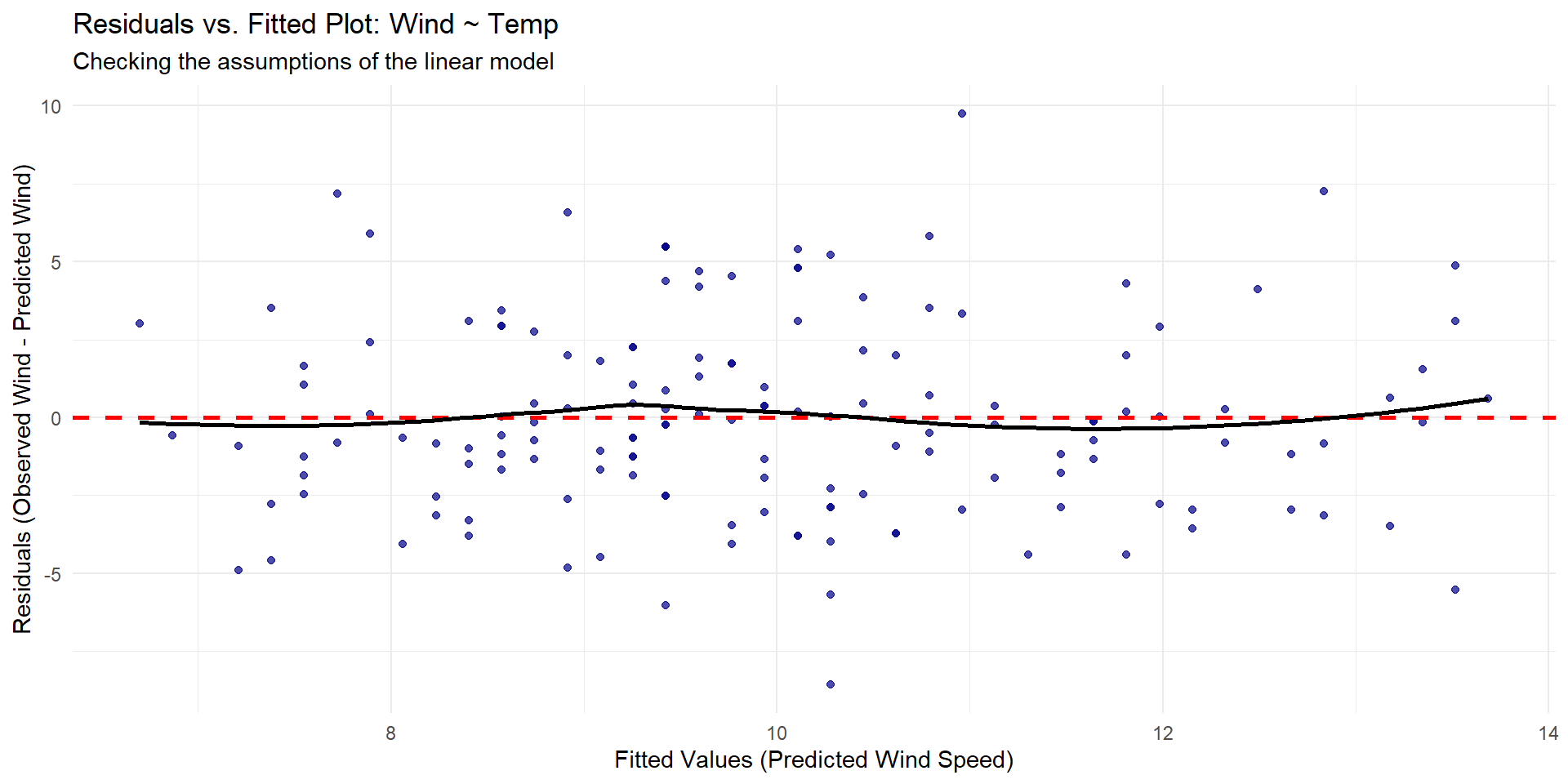
Residual vs Fitted (Predicted)

Violation of linearity

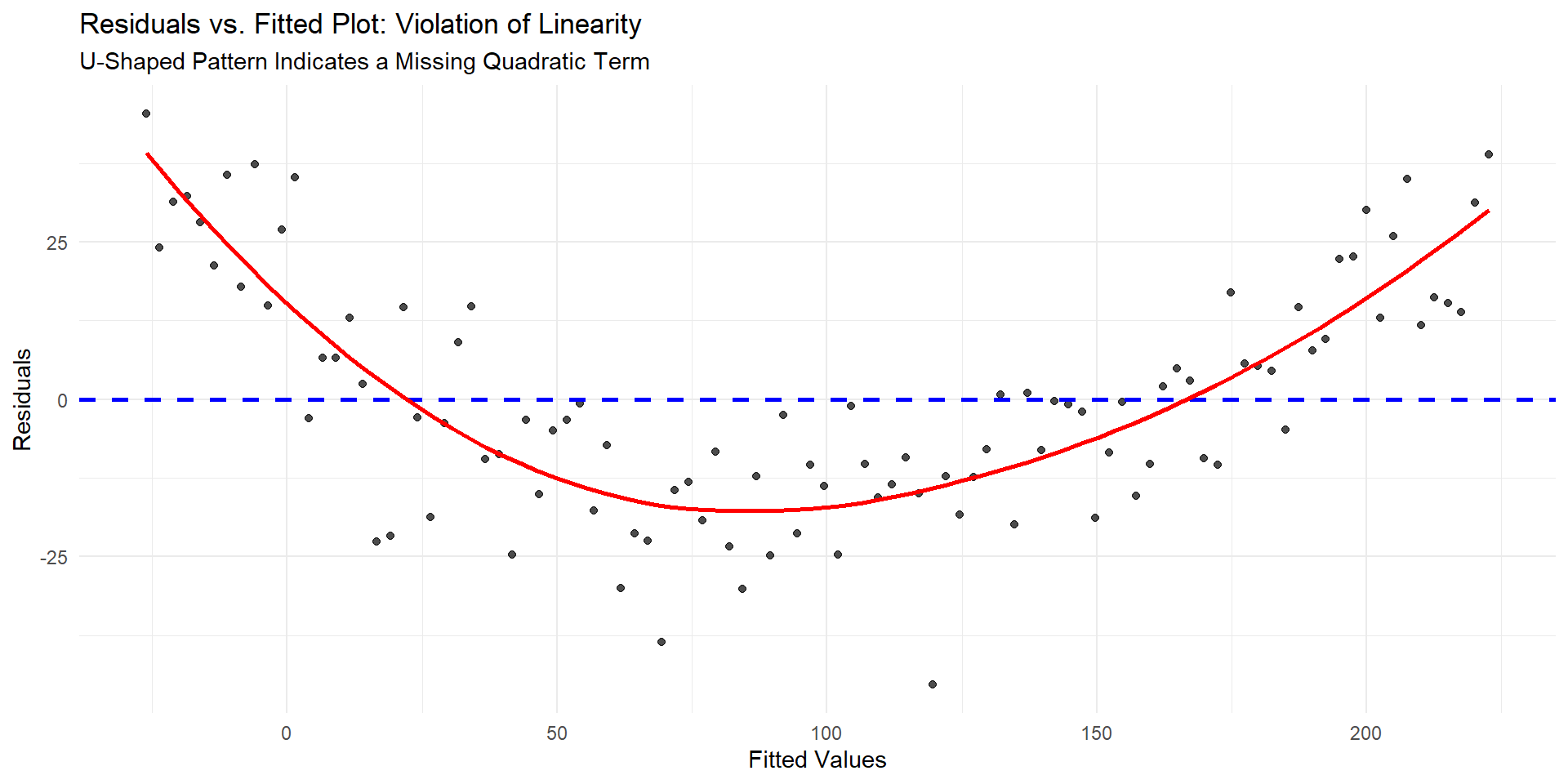
Residual vs Fitted (Predicted)

Checking Equal Variance!

Violation of Equal Variance

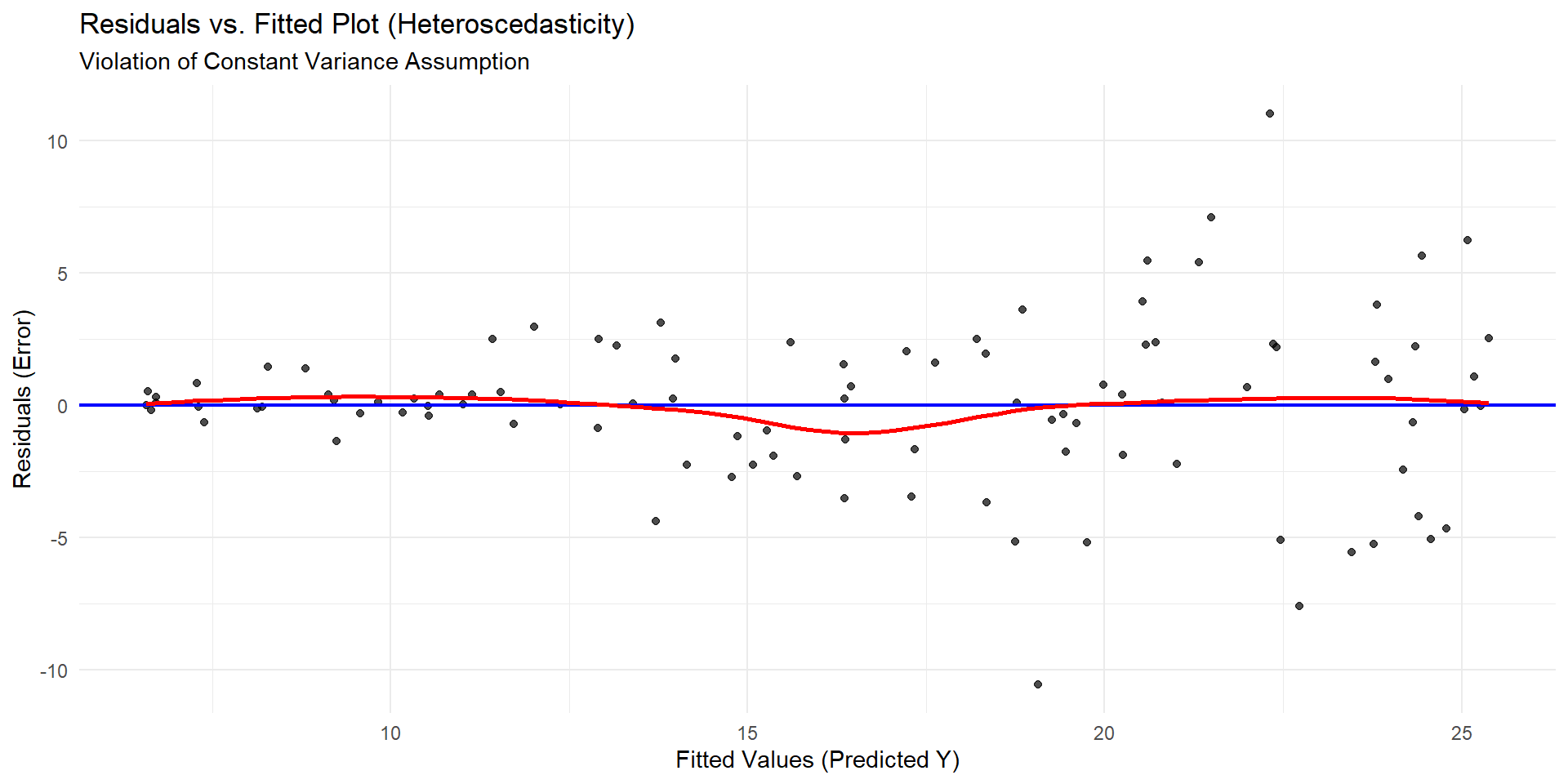
In Summary

Normality

We think about our sample size and also look at Normal Q-Q plots!

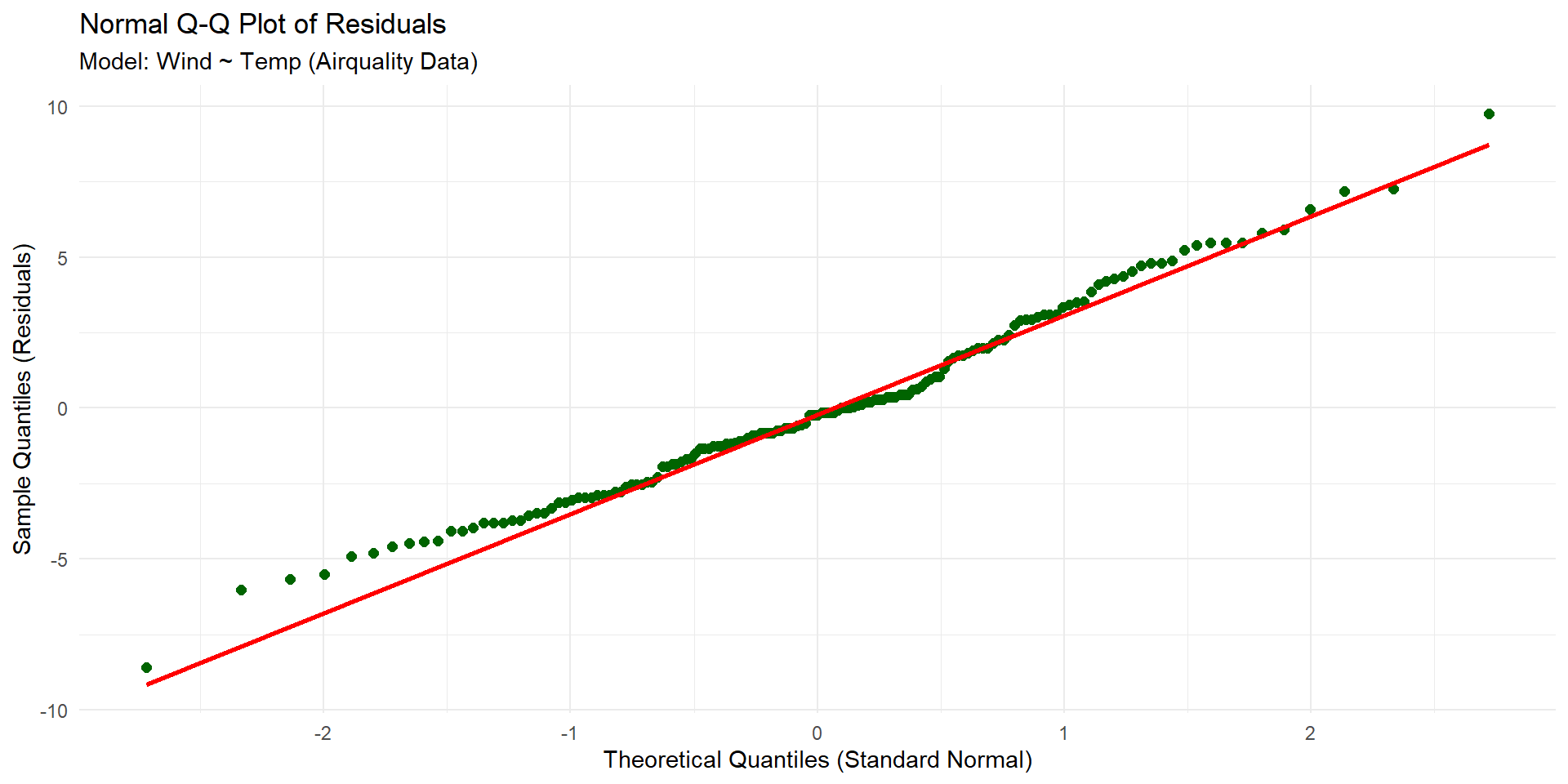
In R

plot(model1) # use plot around your lm object

Test statistic

t

… (yes this is the entire slide….)

Test statistic

\[t = \frac{\hat{\beta}_1 - \beta_{\text{null}}}{\text{SE}(\hat{\beta}_1)}\]

Standard Error

\[\text{SE}(\hat{\beta}_1) = \sqrt{\frac{\text{Unexplained Variation in } Y \text{ (due to error)}}{\text{Variation/Spread in } X \text{}}}\]

\[\text{SE}(\hat{\beta}_1) = \sqrt{\frac{\hat{\sigma}^2}{\sum_{i=1}^{n} (X_i - \bar{X})^2}}\]

\[\hat{\sigma}^2 = \frac{\text{RSS}}{n - 2}\]

\[\hat{\sigma}^2 = \frac{\sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2}{n-2}\]

Output

term estimate std.error statistic p.value
(Intercept) 23.234 2.112 10.999 0
Temp -0.170 0.027 -6.331 0

And this t-statistic follows a t-distribution with n-2 degrees of freedom (-2 because we estimate the population slope and intercept)

– Recreate the statistic

– Draw out what the p-value would look like

What does all of this mean?

Confidence intervals

We can calculate two types of confidence intervals:

– Confidence interval for the mean response (what we will cover)

– Confidence interval for the slope (next time)

– Prediction interval for a brand new observation

Output

term estimate std.error statistic p.value
(Intercept) 23.234 2.112 10.999 0
Temp -0.170 0.027 -6.331 0

Suppose I want to predict the true mean Wind (mph) for when the Temp is 17 degrees.

Do it!

Do you think this is the true value?

Response

\(\hat{\mu_y} \pm t^* * SE_\hat{\mu_y}\)

Standard Errors

\(X_\text{given}\) = What we set x equal to

\[\text{SE}_{\hat{\mu}_{Y}|X_g} = \sqrt{\hat{\sigma}^2 \left[\frac{1}{n} + \frac{(X_\text{given} - \bar{X})^2}{\sum_{i=1}^{n} (X_i - \bar{X})^2}\right]}\]

Terms

The term \(\frac{1}{n}\) accounts for the general uncertainty in estimating the intercept

The term \(\hat{\sigma}^2\) in the outer square root represents the uncertainty around our prediction.

\(\left(\frac{(X_{\text{given}} - \bar{X})^2}{\sum_{i=1}^{n} (X_i - \bar{X})^2}\right)\) accounts for the uncertainty introduced by the slope (\(\hat{\beta}_1\)).

Review

What happens to these intervals when…

– n goes up?

– Confidence level goes down?

In R

model1 <- lm(Wind ~ Temp, data = airquality)

new_temp_data <- tibble(Temp = 17)

predict(
  model_fit, 
  newdata = new_temp_data, 
  interval = "confidence", 
  level = 0.95
)
       fit      lwr      upr
1 20.33579 17.05817 23.61342

Questions?

🔗 class website