Logistic Regression II
NC State University
ST 511 - Fall 2025
2025-11-19
Checklist
– HW 6 released today (due November 30th at 11:59pm)
– Quiz 11 (released Wednesday; due Sunday)
– Don’t forget about the statistics experience
– Final Exam is Dec 8th at 3:30
– We will finish the AE we did Monday. Don’t reclone it! Just open it in your RStudio!
Homework 6
– Can you read in data (extension?)
– Logistic regression
– Make a prediction
– Make a prediction interval (extension)
Course evaluations
We are going to take 5-minutes to fill out the course evaluation: http://go.ncsu.edu/cesurvey
These are important!
I take them very seriously, and will read them after the semester The department takes them very seriously
You are my favorite class I’ve ever taught at NC State!

Regression
– Simple linear regression
– Multiple linear regression (additive)
– Multiple linear regression (interaction)
– Logistic regression
Logistic regression
Why can’t we use linear regression with a categorical response variable?
The problem
Response variable can only take on values of 0 or 1.
(\(\mu_y\)) = (\(\beta_0 + \beta_1 X_1 + \dots\))
The right side of a regression equation, which can take any value from \(-\infty\) to \(+\infty\).
(\(\mu\)): The expected value of the response variable, which is restricted to a certain range
The plot
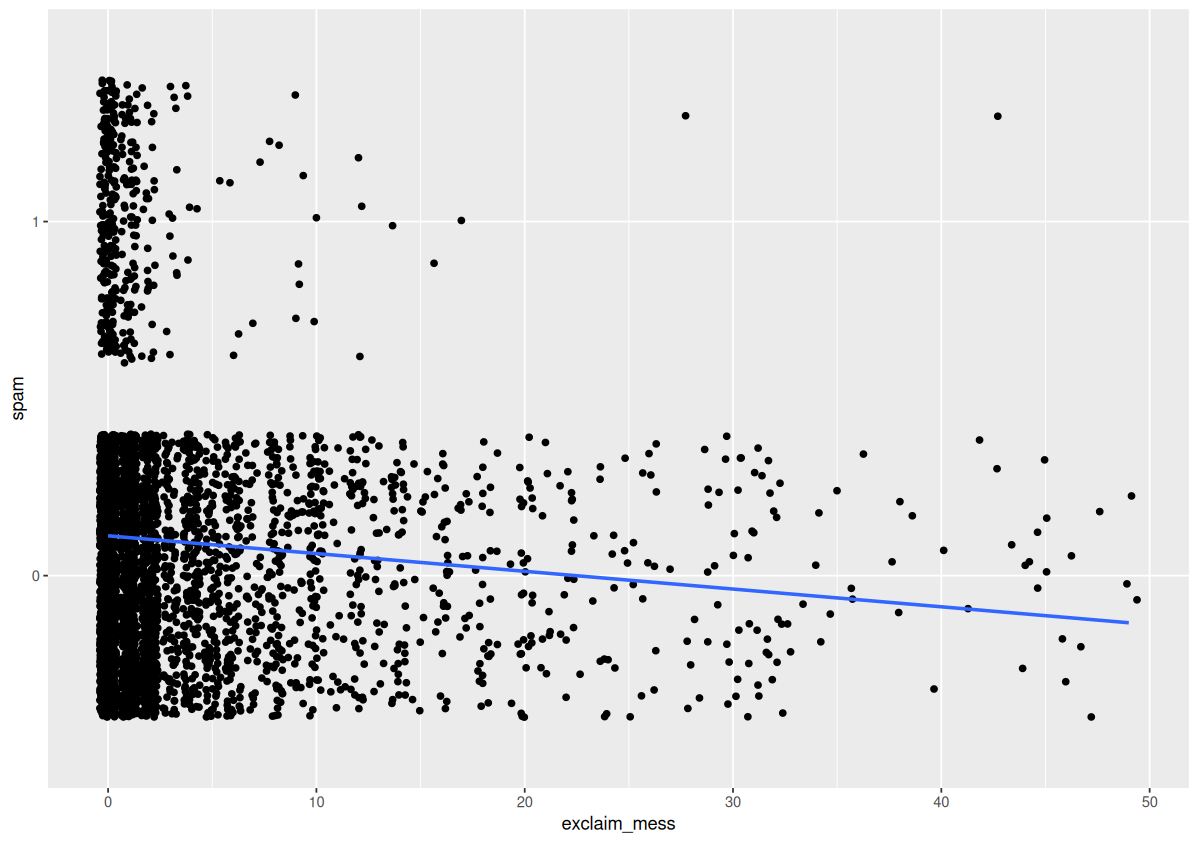
Instead
(\(\mu_y\))
we perform a mathematical transformation and our response is
\(ln(\frac{p}{1-p})\)
Logistic regression
\(ln(\frac{p}{1-p}) = \beta_o + \beta_1x_1+ ....\)
\(\widehat{ln(\frac{p}{1-p}}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
Logistic regression
\[\hat{p} = \frac{e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}{1 + e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}\]
Model
Example Figure:
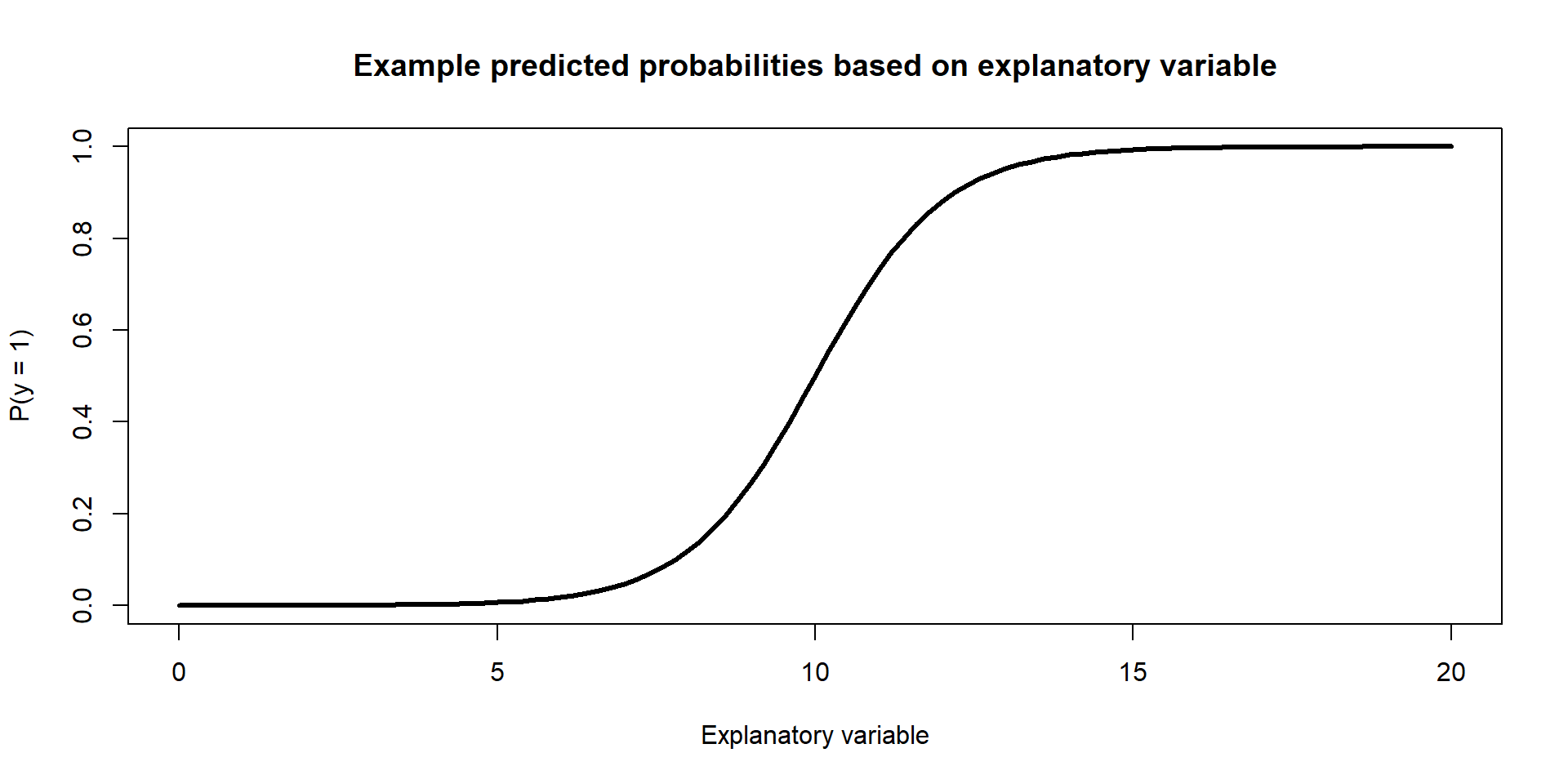
What can we do with this model
– Make predictions (same as linear regression) <- what we will cover
– We can make intervals around this prediction (same as linear regression but we didn’t cover it; see homework)
– You can test coefficients (just like linear regression, but the test statistic is different; Wald test that using a chi-square statistic; we won’t cover this)
– You can create confidence intervals for coefficients (just like linear regression; we won’t cover this)
Questions?
Finish AE
If Time
We have spent a lot of time talking about inference
Sometimes, you want to compare how well your models predict
Let’s talk through how you could do this, so you have an understanding of the process if you so need it.
