Difference in Means

Dr. Elijah Meyer

NC State University
ST 511 - Fall 2025

2025-10-06

Checklist

– Exam Wednesday

  See announcement on Moodle 
  Today's info will be on exam-1

– Take-home released shortly after

– No Quiz this week

– AE solutions posted

– Homework-3 key posted tomorrow morning

Warm-up

A pharmaceutical company has developed a new, cheaper flu vaccine. To gain approval, they must demonstrate that it is effective for a significant proportion of the population, specifically that its protection rate is higher than 80% (the established industry standard for existing vaccines).

What is the null and alternative hypothesis for this study?

Warm-up

A baseball team analyst wants to determine if their star pitcher, Alex, has experienced a statistically significant decline in his strikeout rate between last season and the current season.

The “success” is defined as a pitch resulting in a strike.

Last Time

We are going to look at Gentoo penguins. It is assumed that Gentoo penguins historically weigh, on average, 6500 grams. You want to test if the Gentoo penguins on an island in Palmer Archipelago, are different than what is historically known.

p-value

\(t = \frac{5076 - 6500}{504/\sqrt{123}} = −31.335\)

Confidence interval

\(\bar{x_1}\pm t^* * SE(\bar{x_1})\)

6500 \(\pm\) 1.9796 * 45.444

(6410.039, 6589.961)

Relationship between hypothesis testing and confidence intervals

Does 6500 seem like a plausible value? Why or why not?

If the confidence level and \(\alpha\) value “match up” (ex. \(\alpha\) = 0.05 and 95% confidence interval)…

If the hypothesis test leads you to reject the null hypothesis, it means that the distance between \(\bar{x}\) and \(\mu_o\) is greater than the margin of error defined by the 95% CI.

The margin of error for the confidence interval is also the width of the “non-rejection” region.

The math

\(\left| \frac{\bar{x}_1 - \bar{x}_2}{SE} \right| > t^*\)

\(|\bar{x}_1 - \bar{x}_2| > t^* \times SE\)

This inequality states that the distance from the center of the interval to the null value is greater than the margin of error. If the distance to the null is longer than the margin of error around the sample mean, the confidence interval must exclude the null.

Relationship between hypothesis testing and confidence intervals

These two equations are mathematically equivalent, proving that rejecting \(H_o\) is the same as the confidence interval excluding the null value.

Questions

New Context: Same stuff!

Palmer Penguins

Data were collected and made available by Dr. Kristen Gorman and the Palmer Station, Antarctica LTER, a member of the Long Term Ecological Research Network.

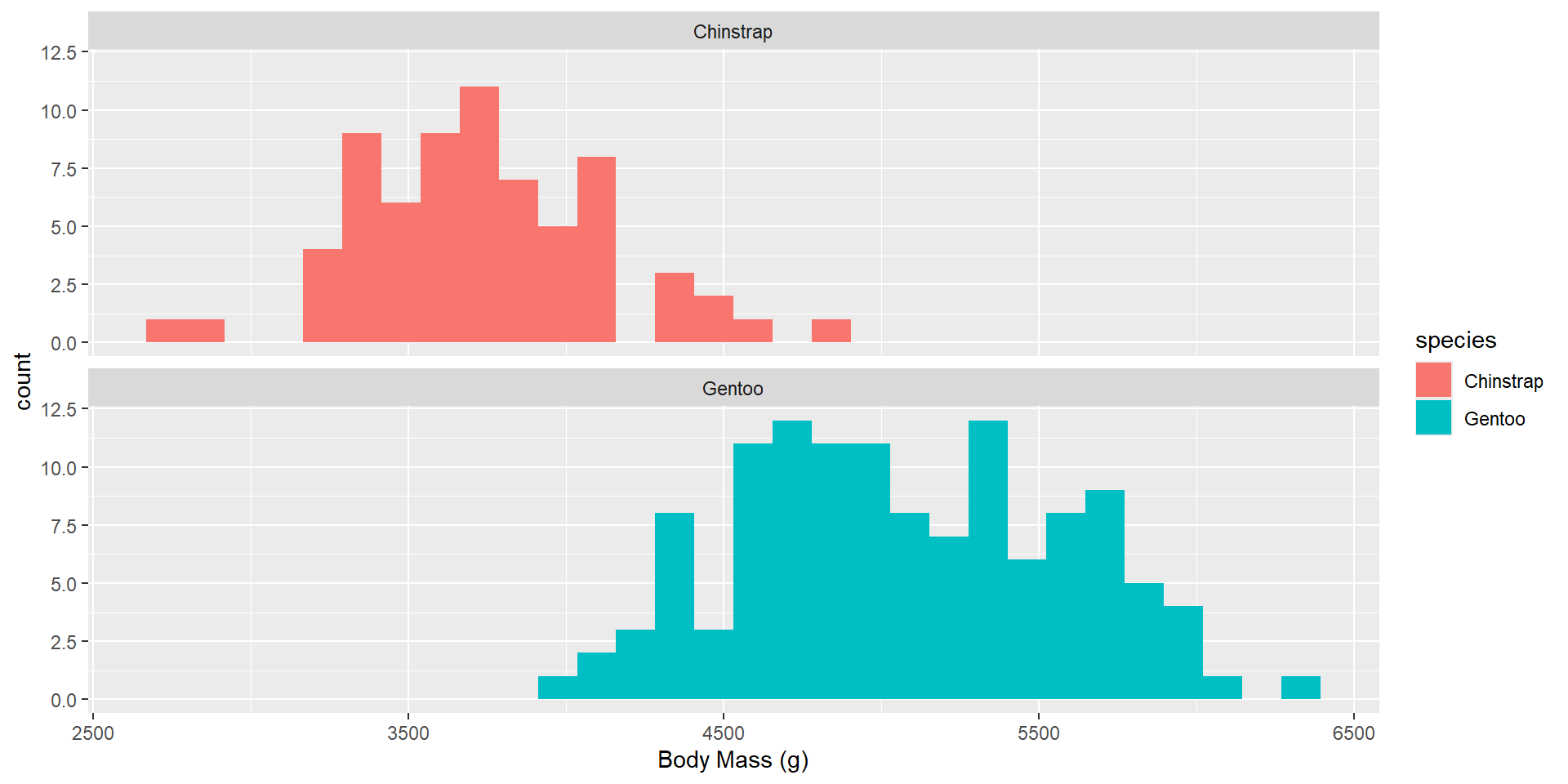
The penguins data set has size measurements for adult foraging penguins near Palmer Station, Antarctica. We want to investigate if the Gentoo penguins have a different body mass than the Chinstrap penguins.

What is our null and alternative hypothesis?

What is the proper notation for our statistic?

The Data

# A tibble: 2 × 3
  species    mean  size
  <fct>     <dbl> <int>
1 Chinstrap 3733.    68
2 Gentoo    5076.   124

What do we need to check?

The Assumptions

When we have two groups, we check both groups!

How do we feel?

our test-statistic

standard deviation

Calculate our t-statistic below

# A tibble: 2 × 4
  species   mean_bm    sd  size
  <fct>       <dbl> <dbl> <int>
1 Chinstrap   3733.  384.    68
2 Gentoo      5076.  504.   124

t-statistic

\[t = \frac{(5076 - 3733) - 0}{\sqrt{\frac{504^2}{124} + \frac{384^2}{68}}} = 20.68\]

Draw/think about what our p-value looks like!

What is our decision? What is our conclusion?

Questions?

Confidence intervals

Reminder

When do we make confidence intervals?

Margin of error

best guess \(\pm\) margin of error

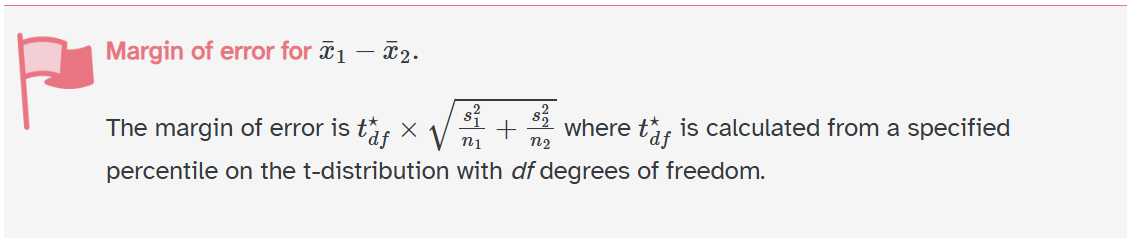
Confidence Interval

1343 \(\pm\) 1.996 * 64.94 = (1213.38, 1472.62)

How can we interpret this?

Interpretation

We are 95% confident that the true mean bodymass for the Gentoo penguins is 1213.38 to 1472.62 grams HIGHER than the true mean body mass for the Chinstrap penguins.

🔗 class website